Estadística Multivariada

class: bottom, left

<!---
Para correr en ATOM
- open terminal, abrir R (simplemente, R y enter)
- rmarkdown::render('8_compmodel.Rmd', 'xaringan::moon_reader')

About macros.js: permite escalar las imágenes como [scale 50%](path to image), hay si que grabar ese archivo js en el directorio.
--->

.right[![:scale 30%](https://escudouchile.files.wordpress.com/2012/06/logotipo-facso-ciencias-sociales-u-de-chile.png)]

# Estadística multivariada, 1 sem. 2019

## Juan Carlos Castillo & Alejandro Plaza

## **Sesión 8**: Interpretación y comparación de modelos

---
class: inverse

# Contenidos

## 1. Repaso de sesión anterior

## 3. Inferencia Estadística (continuación)

## 4. Comparación ajuste de modelos

## 5. Comparación de variables independientes

---
class: inverse, middle, center

# 1. Repaso sesión anterior

---
## Predictores categóricos dicotómicos

- Pensemos que queremos predecir el ingreso de una persona, a partir de una variable `$X$` dicotómica o _dummy_, que expresa el sexo de una persona

`$$X=1(Mujer)$$`
`$$X=0(Hombre)$$`

--
Sustituyendo en la ecuación de regresión:

- Para las mujeres: `$Y=\alpha +\beta X= \alpha+\beta$`

- Para los hombres: `$Y=\alpha +\beta X= \alpha$`

### El coeficiente `$\beta$` expresa las diferencias promedio en `$Y$` (ej: ingreso) entre los grupos.

---
## Predictores categóricos múltiples (politómicos)

- Extensión del caso dicotómico

- se transforman todas las categorías a variables _dummy_

- una de las categorías se deja fuera del modelo de regresión y se utiliza como referencia para la interpretación

|                 | `$X_{media}$` | `$X_{tecnica}$` | `$X_{universitaria}$` |
|------------------|---------|------------|-----------------|
| Básica           | 0       | 0          | 0               |
| Media            | 1       | 0          | 0               |
| Técnica Superior | 0       | 1          | 0               |
| Universitaria    | 0       | 0          | 1               |

`$$Y_{ingreso} = \beta_{0}+\beta_{1}X_{media}+\beta_{2}X_{tecnica}+\beta_{3}X_{universitaria}$$`

---
.pull-left[
### Resumen categóricos
.medium[
- Podemos incluir variables explicativas categóricas incluyéndolas en el modelo como un conjunto de variables dicotómicas 1/0 (dummy).

- Una variable binaria por cada categoría, excepto por una **categoría de referencia**.

- La interpretación de los coeficientes es la diferencia en promedio entre la categoría y la categoría de referencia, manteniendo el resto de las variables constantes.

- La selección de la categoría de referencia suele ser arbitraria y no genera una diferencia sustantiva en el modelo, pero ojo que determina cual es la unidad de agrupamiento y por ende su interpretación.
]
]

.pull-right[
### Modelo de regresión lineal:

.small[

<table cellspacing="0" align="center" style="border: none;">
<caption align="bottom" style="margin-top:0.3em;"> </caption>
<tr>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;"></th>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;">Modelo 1</th>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;">Modelo 2</th>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Intercepto</td>
<td style="padding-right: 12px; border: none;">4.59***</td>
<td style="padding-right: 12px; border: none;">3.36***</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.11)</td>
<td style="padding-right: 12px; border: none;">(0.14)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Edad</td>
<td style="padding-right: 12px; border: none;">-0.00</td>
<td style="padding-right: 12px; border: none;">0.01***</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.00)</td>
<td style="padding-right: 12px; border: none;">(0.00)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Ingreso</td>
<td style="padding-right: 12px; border: none;">0.00*</td>
<td style="padding-right: 12px; border: none;">0.00*</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.00)</td>
<td style="padding-right: 12px; border: none;">(0.00)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Mujer</td>
<td style="padding-right: 12px; border: none;">-0.13*</td>
<td style="padding-right: 12px; border: none;">-0.07</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.06)</td>
<td style="padding-right: 12px; border: none;">(0.06)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Media</td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">0.60***</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.08)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Técnica</td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">1.07***</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.10)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Universitaria</td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">1.37***</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.10)</td>
</tr>
<tr>
<td style="border-top: 1px solid black;">R2</td>
<td style="border-top: 1px solid black;">0.01</td>
<td style="border-top: 1px solid black;">0.08</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Adj. R2</td>
<td style="padding-right: 12px; border: none;">0.00</td>
<td style="padding-right: 12px; border: none;">0.08</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Num. obs.</td>
<td style="padding-right: 12px; border: none;">2339</td>
<td style="padding-right: 12px; border: none;">2337</td>
</tr>
<tr>
<td style="border-bottom: 2px solid black;">F statistic</td>
<td style="border-bottom: 2px solid black;">4.80</td>
<td style="border-bottom: 2px solid black;">35.93</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;" colspan="4">***p &lt; 0.001, **p &lt; 0.01, *p &lt; 0.05., errores estándar en paréntesis</td>
</tr>
</table>
]
]

---

## Inferencia: Prueba de hipótesis

Contraste de la *hipótesis nula*:

`$$H_{0}: \beta_{j} = 0$$`

En relación a la siguiente hipótesis alternativa:

`$$H_{a}: \beta_{j} \neq 0$$`
Lo que implica que:

`$H_{0}$`: **No** hay asociación lineal entre el predictor `$X$` y la variable `$Y$` en la población.

`$H_{a}$`: **Hay** asociación lineal entre el predictor `$X$` y la variable `$Y$` en la población.

---
## Inferencia, diferencias y prueba _t_

- La prueba _t_ se utiliza para inferencias sobre diferencias entre grupos, y básicamente es una razón entre

.center[![:scale 60%](../images/t1.png)]

- Ya que la diferencia esperada si `$H_0$` es verdadera es 0, entonces es la diferencia observada dividida por el error estándar de la diferencia entre los promedios:

`$$t=\frac{b_j}{SE(b_j)}$$`

- Luego este estadístico se contrasta con los valores críticos de la tabla _t_, para el nivel de confianza establecido (usualmente a 95% o 99%).

---
## Inferencia y tabla de regresión

.pull-left[.small[

.pull-right[
- En la tabla lo que aparece en paréntesis bajo los `$\beta$` es usualmente el Error Estándar `$SE(b_j)$`

- El estadístico _t_ se obtiene entonces dividiendo `$\beta$` por su `$SE(b_j)$`, y a esto se asocia un nivel de confianza para la probabilidad de error del rechazo de `$H_0$`, que se refleja en las estrellas, usualmente ``*p<0.1; **p<0.05; ***p<0.01`

]
---
## Inferencia e Intervalos de confianza

- Los **Intervalos de Confianza** proporcionan un rango de valores posibles para el parámetro poblacional.

- Este rango nos permite reflejar en qué medida el `$\beta$` es estadísticamente distinto de 0 para un cierto nivel de confianza

- El rango se construye sumando y restando un Error Estándar ponderado

`$$IC=\beta_{j}\pm c*SE(\hat{\beta{j}})$$`
donde `$c$` representa el percentil en la distribución `$t_{n-k-1}$`.

- El ponderador `$c$` depende de
  - 1) el nivel de confianza con el cual queramos construir el intervalo, y
  - 2) si la hipótesis es direccional o bidireccional.

Con esta información se obtiene el valor critico de la tabla de valores _t_ (o automáticamente en con la función `confint`)

---
## Ejemplo intervalo de Confianza

- Nos interesa el efecto de educación universitaria($\beta$) en ingreso, y tenemos que:
-
 - `$\beta$`=1.368
 - `$SE$`=0.1037
 - Ponderador: valor crítico de _t_ para p<0.025 (0.05/2 por hipótesis bidireccional), con N-k-1 (N=2,337, k regresores=6) df: 2,330=1,9609

En este caso, estimamos el intervalo al 95% de confianza a dos colas, obtenemos lo siguiente:

`$$LimiteSuperior= 1.368 + 1.9609*0.1037=1.57$$`
`$$LimiteInferior= 1.368 - 1.9609*0.1037=1.17$$`

**Interpretación**: en ninguno de los límites el `$\beta$` "atraviesa" el cero, por lo que se puede rechazar con el 95% de confianza que `$\beta = 0$`

---
## Visualización  de intervalos de confianza

![](8_compmodel_files/figure-html/unnamed-chunk-4-1.png)

---
# Resumen

- Inferencia sobre los coeficientes de regresión: ¿puedo decir que el efecto de `$\beta$` es distinto de 0?¿con qué probabilidad?

--
- Obtención de valor _t_: `$\beta$` dividido por su error estándar

- Comparación con valor críticos de t según nivel de confianza (ej: 95%) y grados de libertad del modelo (n-k-1)

- Información aparece ya resumida en tabla de regresión con "estrellas" para distintos niveles de confianza

- Construcción de intervalos: permite una apreciación más detallada de la significación de los coeficientes, también en comparación a otros coeficientes

---
class: inverse, middle,center

# PREGUNTAS

---
class: inverse, middle,center

# 2. Inferencia (Continuación)

---
# Prueba de hipótesis para el modelo

- Sesión anterior: inferencia para cada `$\beta$` por separado

- ¿Cómo demostramos que el modelo en conjuto es significativo estadísticamente?

- Para probar que el conjunto de coeficientes de las variables independientes son diferentes de 0, se utiliza una prueba de ajuste global: **La prueba F**.

---

## Prueba F

La prueba F es usada para probar una hipotesis multi-coeficientes de la siguiente forma:

`$$H_{0}: \beta_{1}=\beta_{2}=...=\beta_{k}=0$$`
en contra de la siguiente alternativa, donde al menos un coeficiente es diferente de 0

`$$H_{a}: \beta_{1},\beta_{2},...,\beta_{k}\neq0$$`

---

##Prueba F

La prueba F es la razón entre la varianza explicada del modelo y la no explicada, que también se podría expresar:

`$$F= \frac{Varianza_{Explicada}}{Varianza_{NoExplicada}}$$`

Las varianzas explicadas (modelo) y no explicadas (residuos) se obtienen de la siguiente manera:

`$$F=\frac{MS_{regresion}}{MS_{residuos}}=\frac{\sum({\hat{Y_{i}}-\bar{Y_{i}}})^2/k}{\sum({Y_{i}-\hat{Y_{i}}})^2/N-k-1}$$`

Donde `$MS_{regresion}$` es la media de los residuos de la regresión al cuadrado, y  `$MS_{residuos}$` es la de los residuos

Al igual que con _t_, se obtiene un valor crítico de _F_ para un cierto nivel de confianza,  que luego se contrasta con el calculado.
---
# Prueba F (tabla ANOVA)

`$$F=\frac{MS_{regresion}}{MS_{residuos}}=\frac{\sum({\hat{Y_{i}}-\bar{Y_{i}}})^2/k}{\sum({Y_{i}-\hat{Y_{i}}})^2/N-k-1}$$`

.medium[

| Fuente de Y | Suma de cuadrados (SC) | df | Media de suma de cuadrados (MS) | F |
|-----------|------|-------|--------------------|------------|
| Regresion | `$\sum({\hat{Y_{i}}-\bar{Y_{i}}})^2$` | `$k$` | `$SC_{regresion}/k$` | `$MS_{regresion}/$` `$MS_{residual}$` |
| Residual | `$\sum({Y_{i}-\hat{Y_{i}}})^2$` | `$n-k-1$` | `$SC_{residual}/(n-k-1)$` | |
| Total | `$\sum({Y_{i}-\bar{Y_{i}}})^2$` | `$n-1$` | | |

]

---
# Ejemplo prueba F

Predecir el salario de los jugadores en base a los años de experiencia y los partidos jugados al año (Wooldridge 2006, Sección 4.5 - datos: MLB1.DTA)

```
## 
## Call:
## lm(formula = lsalary ~ years + gamesyr, data = mlb1)
## 
## Residuals:
## Min 1Q Median 3Q Max 
## -2.66858 -0.46412 -0.01176 0.49219 2.68829 
## 
## Coefficients:
## Estimate Std. Error t value Pr(>|t|) 
## (Intercept) 11.223804 0.108312 103.625 < 2e-16 ***
## years 0.071318 0.012505 5.703 2.5e-08 ***
## gamesyr 0.020174 0.001343 15.023 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7527 on 350 degrees of freedom
## Multiple R-squared: 0.5971,	Adjusted R-squared: 0.5948 
## F-statistic: 259.3 on 2 and 350 DF, p-value: < 2.2e-16
```

---
# Calculo de F paso a paso

1- Estimamos `$\hat{Y}$`, el salario predicho

```r
mlb1$salary_estimado<- fitted(model1)
```

2- Suma de los cuadrados de la Regresion `$\sum({\hat{Y_{i}}-\bar{Y_{i}}})^2$` y Suma de los cuadrados residuales `$\sum({Y_{i}-\hat{Y_{i}}})^2$`

```r
ss_reg<-sum((mlb1$salary_estimado-mean(mlb1$lsalary))^2)
ss_res<-sum((mlb1$lsalary-mlb1$salary_estimado)^2)
```

3- Media de las sumas de cuadrados, según sus respectivos grados de libertad

```r
MS_reg<- ss_reg/2 #2 predictores
MS_res<- ss_res/(353-2-1) #(n-k-1)
```
---

4 - Razón de estas dos medias es el puntaje F

```r
(F_score<-MS_reg/MS_res)
```

```
## [1] 259.3204
```

---
# Inferencia en base a F

5 - Comparación con valor crítico de F para un 95% de Confianza

```r
qf(0.95,350,2)
```

```
## [1] 19.49287
```

El valor de F es mucho más alto que el valor crítico de F, por lo que se rechaza la hipótesis nula de que al menos uno de los coeficientes es igual cero.

### En conclusión:
La prueba F es una medida general de ajuste que nos permite establecer con un grado de probabilidad convencional (ej: 95%) si nuestro modelo es estadísticamente significativo.

???
lsalary = log de salario
years = años en las ligas mayores
gamessyr = Juegos de carreras hechas por años
bavg    = promedio de bateo
hrunsyr = Homeruns (cuadrangulares) por año
rbisyr = carreras impulsadas por año

---
class: inverse, middle, center

# 3. Comparación de modelos

---

## Sobre comparación de modelos

Hasta ahora hemos aprendido a especificar modelos y también establecer criterios de significación estadística a nivel de predictores y del modelo completo. Pero, ¿cuál es el mejor modelo que podemos presentar?

### Criterio Sustantivo:

+ ¿Cuán interesante es para responder nuestra pregunta de investigación?

+ ¿Cómo podemos trasladar este interés a decisiones sobre qué variables incluir/excluir, y cómo (re)codificamos estás variables?

### Criterio Estadístico

+ ¿Cuál modelo predice de mejor manera la variable dependiente?

+ ¿Qué modelo nos permite rechazar la hipótesis nula (según _t_ o _F)?

---
## Sobre comparación de modelos

2 formas generales de comparar modelos

- Varianza explicada de la variable dependiente: `$R^2$`

- Diferencias de ajuste estadístico: Prueba *F*

---
## Varianza explicada: R2

Recordando de la [Sesión 4](https://juancarloscastillo.github.io/metsoc-facsouchile/documents/presentaciones/4regsimp2/4_regsimp2.html#18):

`$$SS_{tot}=SS_{reg} + SS_{error}$$`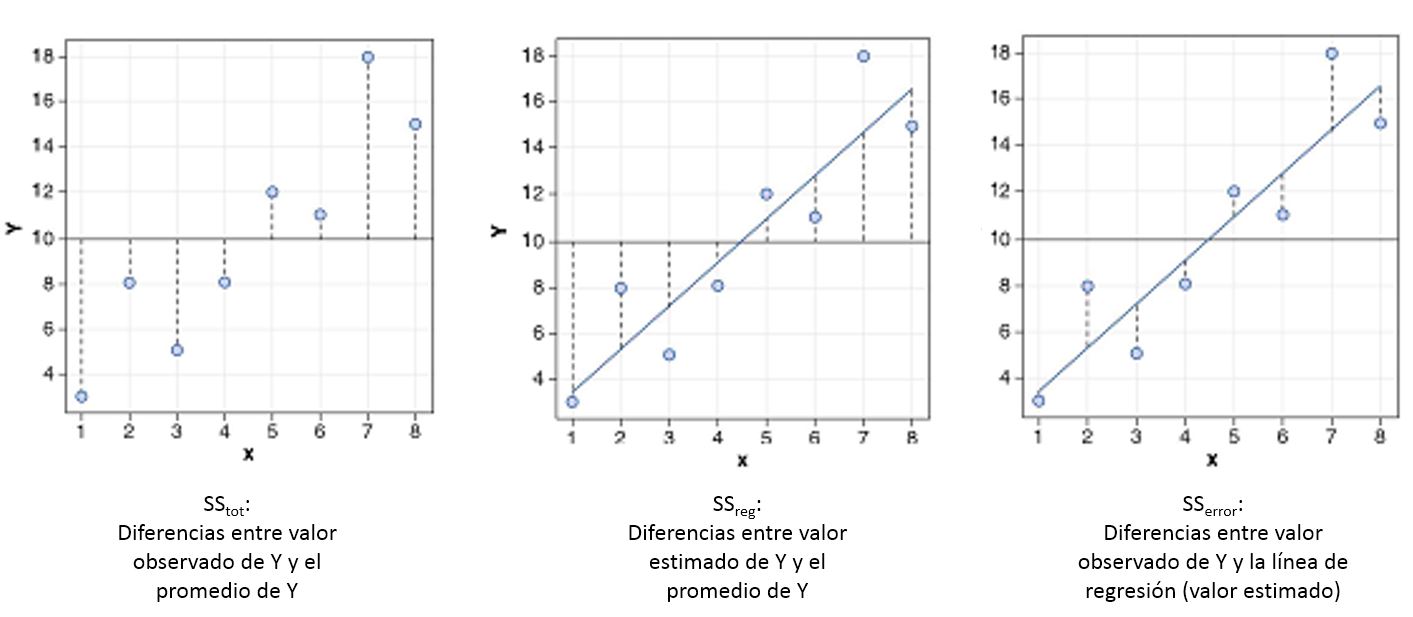

![image](../images/resid_3.JPG)

---
# Varianza explicada: R2

Por lo tanto:

`$$SS_{tot}=SS_{reg} + SS_{error}$$`

`$$\frac{SS_{tot}}{SS_{tot}}=\frac{SS_{reg}}{SS_{tot}} + \frac{SS_{error}}{SS_{tot}}$$`

`$$1=\frac{SS_{reg}}{SS_{tot}}+\frac{SS_{error}}{SS_{tot}}$$`

`$$\frac{SS_{reg}}{SS_{tot}}= 1- \frac{SS_{error}}{SS_{tot}}=R^2$$`

---
## R2 ajustado

- La comparación de modelos por `$R^2$` es limitada ya que esta magnitud siempre aumentará cuando se agreguen más variables explicativas, aún cuando su aporte no sea significativo.

- Para ello se realiza una corrección: `$R^2_{adj}$`:

`$$R^2_{adj}=R^2 -\frac{k(1-R^2)}{N-k-1}= 1- \frac{N-1}{N-k-1}(1-R^2)$$`

Este coeficiente **penaliza** por la cantidad de variables incluidas en el modelo al integrar el término `$k$` (número de variables)

Por lo tanto, al momento de comparar `$R^2$` entre modelos se debe considerar el ajustado

---
## Diferencias de ajuste estadístico: Prueba F

Bajo la prueba F, la hipótesis nula y alternativa se especifican para dos modelos lineales de `$Y$` de la siguiente manera:
`$$M_{0}: y=\beta_{0}+\beta_{1}X_{1}+...+\beta_{g}X_{g}$$`
`$$M_{a}: y=\beta_{0}+\beta_{1}X_{1}+...+\beta_{g}X_{g}+...++\beta_{k}X_{k}$$`
El modelo `$M_{a}$` contiene todas las variables explicativas de `$M_{0}$` más algunas adicionales.

Se podría considerar el modelo `$M_{0}$` como una versión restringida de `$M_{a}$`.

---
## Estadístico F para comparación de modelos

`$$F=\frac{(SRC_{0}-SRC_{a})/q}{SRC_{a}/(n-k_{a}-1)}$$`

Donde

- `$SRC_{a}$` es la suma de los residuos al cuadrado para el modelo completo `$M_{a}$`
- `$SRC_{0}$` suma de residuos al cuadrado para el modelo restringido `$M_{0}$`
- `$q=gl_{a}-gl_{0}$`, es decir, la diferencia de grados de libertad de los modelos
- `$k_{a}=k$` para  `$M_{a}$`.

--
Alternativamente en términos de `$R^{2}$`
`$$F=\frac{R_{a}^2-R_{0}^2}{1-R_{a}}*\frac{n-k-1}{q}$$`

---
## Ejemplo de comparación de modelos con F

.pull-left[.small[

<table cellspacing="0" align="center" style="border: none;">
<caption align="bottom" style="margin-top:0.3em;"> </caption>
<tr>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;"></th>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;">Modelo 1</th>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;">Modelo 2</th>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Intercepto</td>
<td style="padding-right: 12px; border: none;">11.22***</td>
<td style="padding-right: 12px; border: none;">11.19***</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.11)</td>
<td style="padding-right: 12px; border: none;">(0.29)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Años liga</td>
<td style="padding-right: 12px; border: none;">0.07***</td>
<td style="padding-right: 12px; border: none;">0.07***</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.01)</td>
<td style="padding-right: 12px; border: none;">(0.01)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Partidos año</td>
<td style="padding-right: 12px; border: none;">0.02***</td>
<td style="padding-right: 12px; border: none;">0.01***</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.00)</td>
<td style="padding-right: 12px; border: none;">(0.00)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Prom. bateo</td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">0.00</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.00)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Puntos año</td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">0.01</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.02)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Carreras año</td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">0.01</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.01)</td>
</tr>
<tr>
<td style="border-top: 1px solid black;">R2</td>
<td style="border-top: 1px solid black;">0.60</td>
<td style="border-top: 1px solid black;">0.63</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Adj. R2</td>
<td style="padding-right: 12px; border: none;">0.59</td>
<td style="padding-right: 12px; border: none;">0.62</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Num. obs.</td>
<td style="padding-right: 12px; border: none;">353</td>
<td style="padding-right: 12px; border: none;">353</td>
</tr>
<tr>
<td style="border-bottom: 2px solid black;">F statistic</td>
<td style="border-bottom: 2px solid black;">259.32</td>
<td style="border-bottom: 2px solid black;">117.06</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;" colspan="4">***p &lt; 0.001, **p &lt; 0.01, *p &lt; 0.05., errores estándar en paréntesis</td>
</tr>
</table>
]
]

.pull-right[
¿Mejora el modelo al incluir las últimas tres variables?

`$$H_{0}: \beta_{3}=0,\beta_{4}=0,\beta_{5}=0$$`

`$$F=\frac{R_{a}^2-R_{0}^2}{1-R_{a}}*\frac{n-k-1}{q}$$`
`$$F=\frac{0.63-0.60}{1-0.63}*\frac{347}{3}=9.55$$`

Valor crítico para un nivel de confianza de 0.95 con df (3,347)

```
## [1] 2.630641
```
9.55>2.63, rechazamos la hipótesis nula de que el modelo 2 no es distinto del 1.
]

---
## Ejemplo de comparación de modelos con F

Alternativamente en `R`, usando el comando `anova`:

```r
m0<- lm(lsalary~years+gamesyr, data = mlb1 )
ma<- lm(lsalary~years+gamesyr+
 bavg+hrunsyr+rbisyr, data = mlb1)
anova(m0,ma)
```

```
## Analysis of Variance Table
## 
## Model 1: lsalary ~ years + gamesyr
## Model 2: lsalary ~ years + gamesyr + bavg + hrunsyr + rbisyr
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    350 198.31                                  
## 2    347 183.19  3    15.125 9.5503 4.474e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

---
class: inverse, middle, center

# 3. Comparación predictores

---
## Estandarización de Coeficientes

- Recordamos que el `$\beta$` se interpreta como la magnitud del cambio en la variable dependiente `$Y$` producto del cambio en una unidad de las variables independiente `$X_{j}$`.

- Entonces el `$\beta$` está profundamente condicionado a la escala de medición en de las variables independientes `$X_{j}$`.

- ¿Es posible comparar el efecto de distintos variables `$X_{j}$` en `$Y$`?

--
- Para comparar los efectos es necesario transformar las variables a una misma escala, lo que se logra mediante su  **estandarización**

---

## Estandarización de Coeficientes

- La estandarización corresponde a una operación aritmética que se aplica a los valores de la variable, sustrayendo su promedio y dividiendola por su desviación estandar.

###Estandarización para la variable dependiente Y
`$$z_{y}=\frac{y-\bar{y}}{sd(y)}$$`
###Estandarización para la variable independiente X
`$$z_{x_{1}}=\frac{x_{1}-\bar{x_{1}}}{sd(x_{1})}$$`

Donde el modelo se puede expresar como:
`$$z_{y}=\beta_{1}z_{x_{1}} + \beta_{2}z_{x_{2}} +...+z_{x_{j}}$$`
---
class: middle, center

# Al estandarizar, los coeficientes de regresión reflejan cuantas **desviaciones estándar** cambia _Y_ como consecuencia del cambio en **una desviación estándar** _X_.

---
## Estandarización de Coeficientes

1. Paso a paso en `R`:

```r
attach(mlb1)
mlb1$z_lsalary <-(lsalary-mean(lsalary))/sd(lsalary)
mlb1$z_years<- (years-mean(years))/sd(years)
mlb1$z_gamesyr<-(gamesyr-mean(gamesyr))/sd(gamesyr)
```

Y realizamos el modelo de regresión

```r
m0_z1<- lm(z_lsalary~z_years+z_gamesyr, data = mlb1)
```

Alternativamente con `scale()`

```r
m0_z2<- lm(scale(lsalary)~scale(years)+scale(gamesyr), data = mlb1 )
```
---
## Modelo de regresión con variables estandarizadas

.pull-left[.medium[

<table cellspacing="0" align="center" style="border: none;">
<caption align="bottom" style="margin-top:0.3em;"> </caption>
<tr>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;"></th>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;">Model 1</th>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;">Model 2</th>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">(Intercept)</td>
<td style="padding-right: 12px; border: none;">0.00</td>
<td style="padding-right: 12px; border: none;">0.00</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.03)</td>
<td style="padding-right: 12px; border: none;">(0.03)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">z_years</td>
<td style="padding-right: 12px; border: none;">0.23***</td>
<td style="padding-right: 12px; border: none;"></td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.04)</td>
<td style="padding-right: 12px; border: none;"></td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">z_gamesyr</td>
<td style="padding-right: 12px; border: none;">0.62***</td>
<td style="padding-right: 12px; border: none;"></td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.04)</td>
<td style="padding-right: 12px; border: none;"></td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">scale(years)</td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">0.23***</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.04)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">scale(gamesyr)</td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">0.62***</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;"></td>
<td style="padding-right: 12px; border: none;">(0.04)</td>
</tr>
<tr>
<td style="border-top: 1px solid black;">R2</td>
<td style="border-top: 1px solid black;">0.60</td>
<td style="border-top: 1px solid black;">0.60</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Adj. R2</td>
<td style="padding-right: 12px; border: none;">0.59</td>
<td style="padding-right: 12px; border: none;">0.59</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Num. obs.</td>
<td style="padding-right: 12px; border: none;">353</td>
<td style="padding-right: 12px; border: none;">353</td>
</tr>
<tr>
<td style="border-bottom: 2px solid black;">F statistic</td>
<td style="border-bottom: 2px solid black;">259.32</td>
<td style="border-bottom: 2px solid black;">259.32</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;" colspan="4">***p &lt; 0.001, **p &lt; 0.01, *p &lt; 0.05., errores estándar en paréntesis</td>
</tr>
</table>
]]
.pull-right[
En este caso se puede observar que por el aumento en **una desviación estándar** de los años de experiencia de un jugador (z_years), su sueldo aumentará **0.23 desviaciones estándar**.

Al estar en una misma unidad de medida, podemos comparar los coeficientes:

- la cantidad de partidos jugados al año (z_gamesyr) tiene un mayor efecto en el salario en relación a la cantidad de años de experiencia del jugador (z_years).
]

---
class: inverse

# Resumen

## Inferencia Estadística sobre el modelo general:

- ### Prueba F

## Comparación ajuste de modelos:

- ### R2 y R2 ajustado
- ### Prueba F

## Comparación de variables independientes

- ### Estandarización

---

.pull-left[
### Regresión múltiple:
.small[

.pull-right[
### ¿Cómo interpretamos?
.medium[
- Comenzar contando sobre las características de los modelos presentados

- Por modelo
  - foco en hipótesis sustantivas y su contraste con la información sobre significación estadística
  - interpretación más detallada cuando se rechaza la hipótesis nula en relación a los `$\beta$`
  - eventual comparación de coeficientes (ej: estandarización, intervalos de confianza)

- Comparación de modelos
  - `$R^2$` ajustado
  - evantual test de diferencia de modelos
]
]

---

class: bottom, left

.right[![:scale 30%](https://escudouchile.files.wordpress.com/2012/06/logotipo-facso-ciencias-sociales-u-de-chile.png)]

# Estadística multivariada, 1 sem. 2019

## Juan Carlos Castillo & Alejandro Plaza

## **Sesión 8**: Interpretación y comparación de modelos