class: bottom, left <!--- Para correr en ATOM - open terminal, abrir R (simplemente, R y enter) - rmarkdown::render('10_logit2.Rmd', 'xaringan::moon_reader') About macros.js: permite escalar las imágenes como [scale 50%](path to image), hay si que grabar ese archivo js en el directorio. ---> .right[] <br> <br> <br> <br> <br> <br> <br> # Estadística multivariada, 1 sem. 2019 ## Juan Carlos Castillo & Alejandro Plaza ## **Sesión 10**: Regresión Logística 2 --- class: inverse # Contenidos ## 1. Repaso ## 2. Niveles de interpretación ## 3. Ajuste --- class: roja, middle, center # 1. Repasando --- class: inverse, center  # ¿Puedes anticipar el final? ??? Si vas al cine a ver esta película, y si antes conoces los datos sobre el Titanic, puedes anticipar el final? --- # Sobrevivientes .center[ 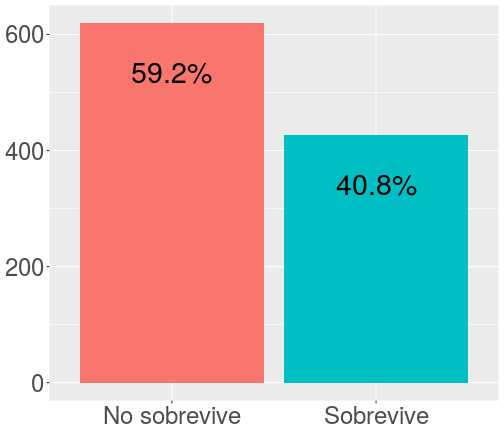<!-- --> ] --- # Sexo .center[ 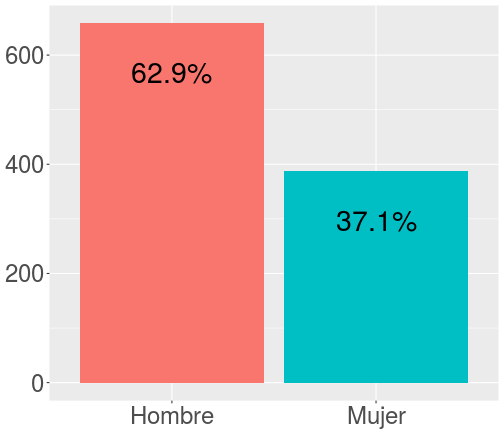<!-- --> ] --- ## Sobrevivencia / sexo .center[ 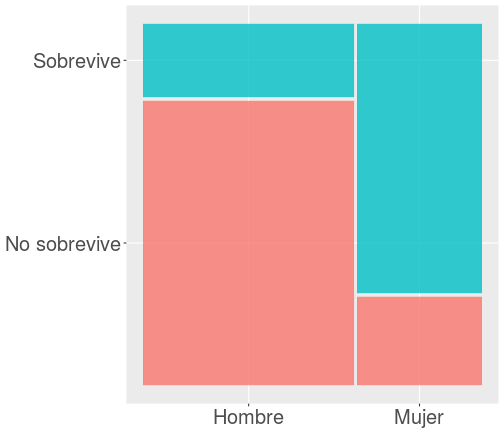<!-- --> ] --- # Sobrevive / Edad .center[ 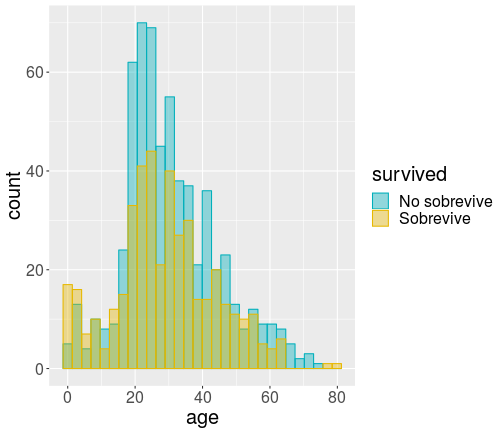<!-- --> ] --- # Regresión ### Modelando la probabilidad de sobrevivir con regresión OLS ```r reg_tit=lm(tt$survived ~ tt$sex) ``` ``` ## Warning in model.response(mf, "numeric"): using type = "numeric" with a ## factor response will be ignored ``` ``` ## Warning in Ops.factor(y, z$residuals): '-' not meaningful for factors ``` -- --- **Primera advertencia**: no se puede hacer una regresión (mínimos cuadrados) con un factor como dependiente. Se puede forzar haciendo "como si" la variable fuera continua con valores 0 y 1. ```r tt <- tt %>% mutate(survived_n=recode(survived, "No sobrevive"=0, "Sobrevive"=1)) ``` --- ## Modelo de probabilidad lineal .pull-left[ Se da este nombre a los modelos de regresión donde una variable dependiente dicotómica se estima de manera tradicional (mínimos cuadrados ordinarios) ] .pull-right[ .medium[ <table style="text-align:center"><tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td><em>Dependent variable:</em></td></tr> <tr><td></td><td colspan="1" style="border-bottom: 1px solid black"></td></tr> <tr><td style="text-align:left"></td><td>survived_n</td></tr> <tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">sex</td><td>0.547^***</td></tr> <tr><td style="text-align:left"></td><td>(0.027)</td></tr> <tr><td style="text-align:left"></td><td></td></tr> <tr><td style="text-align:left">Constant</td><td>0.205^***</td></tr> <tr><td style="text-align:left"></td><td>(0.016)</td></tr> <tr><td style="text-align:left"></td><td></td></tr> <tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td>1,046</td></tr> <tr><td style="text-align:left">R²</td><td>0.289</td></tr> <tr><td style="text-align:left">Adjusted R²</td><td>0.289</td></tr> <tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"><em>Note:</em></td><td style="text-align:right">^*p<0.1; ^**p<0.05; ^***p<0.01</td></tr> </table> ] ] --- ## Significado coeficientes modelo probabilidad lineal .center[ **Promedio de supervivencia por sexo** <!-- html table generated in R 3.6.0 by xtable 1.8-4 package --> <!-- Mon Jun 3 00:06:40 2019 --> <table border=1> <tr> <th> </th> <th> Mean </th> <th> N </th> <th> Std. Dev. </th> </tr> <tr> <td> Hombre </td> <td align="right"> 0.21 </td> <td align="right"> 658 </td> <td align="right"> 0.40 </td> </tr> <tr> <td> Mujer </td> <td align="right"> 0.75 </td> <td align="right"> 388 </td> <td align="right"> 0.43 </td> </tr> <tr> <td> Total </td> <td align="right"> 0.41 </td> <td align="right"> 1046 </td> <td align="right"> 0.49 </td> </tr> </table> ] - El valor del intercepto=0.205 (0.21 aproximado) es el valor predicho para la categoría de referencia "hombre". - El `\(\beta\)` de sexo (mujer) =0.547 sumado al intercepto equivale al promedio de supervivencia de mujeres --- ## Problemas regresión lineal para dependientes dicotómicas .center[ <!-- --> ] --- ## Problemas .... .medium[.center[ <!-- --> ] ] --- # Problemas ... Si hubieran muerto todos los menores de 20 y mayores de 40 ... .medium[.center[ <!-- --> ] ] --- class: roja # Problemas regresión tradicional (OLS) para dependientes dicotómicas - ### Eventuales predicciones fuera del rango de probabilidades posibles - ### Ajuste a los datos / residuos: ¿Es la mejor aproximación una recta? --- class: roja, middle, right ### La regresión logística ofrece una solución a los problemas del rango de predicciones y de ajuste a los datos del modelo de probabilidad lineal -- <br> .center[# ¿Cómo?] -- ## Mediante una _transformación_ de la(s) variable(s) independientes a coeficientes *LOGIT* --- ## OLS vs Logit .pull-left[ <!-- --> ] .pull-right[ <!-- --> ] --- class: roja, middle # 2. Niveles interpretación ## A. Asociaciones e hipótesis ## B. Coeficientes y predicción --- class: inverse, middle, center # A. Asociaciones e hipótesis: ## H1: Las mujeres sobreviven más que los hombres --- # Estimación en R: `glm` Forma general: .large[ ```r modelo <- glm(dependiente ~ indep 1 + indep2 + ..., data=datos, family="binomial") ``` ] -- Similar a regresión OLS con `lm`, diferencias: - `glm` (general lineal model) es la que se utiliza para variables dependientes categóricas - `family="binomial"` indica que la dependiente es dicotómica --- # Ejemplo Titanic .pull-left[ .large[ ```r modelo_titanic <- glm(survived ~ sex, data = tt, family = "binomial") ``` ] ] .pull-right[.medium[ <table style="text-align:center"><tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td><em>Dependent variable:</em></td></tr> <tr><td></td><td colspan="1" style="border-bottom: 1px solid black"></td></tr> <tr><td style="text-align:left"></td><td>survived</td></tr> <tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">sex</td><td>2.467^***</td></tr> <tr><td style="text-align:left"></td><td>(0.152)</td></tr> <tr><td style="text-align:left"></td><td></td></tr> <tr><td style="text-align:left">Constant</td><td>-1.354^***</td></tr> <tr><td style="text-align:left"></td><td>(0.097)</td></tr> <tr><td style="text-align:left"></td><td></td></tr> <tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td>1,046</td></tr> <tr><td style="text-align:left">Log Likelihood</td><td>-551.004</td></tr> <tr><td style="text-align:left">Akaike Inf. Crit.</td><td>1,106.008</td></tr> <tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"><em>Note:</em></td><td style="text-align:right">^*p<0.1; ^**p<0.05; ^***p<0.01</td></tr> </table> ] ] --- ## Interpretación de asociaciones ### - Coeficiente logit asociado a sexo (mujer) = +2.467 : - las mujeres tienen una mayor probabilidad de sobrevivir que los hombres. -- ## Contraste de hipótesis - La diferencia de las probabilidades de sobrevivir entre hombres y mujeres son estadísticamente significativas, por lo que se rechaza la hipótesis nula con un nivel de probabilidad `\(p<0.01\)`. -- ### - Por lo tanto, los coeficientes _logit_ sirven en primera instancia para determinar si existe una asociación positiva o negativa --- class: inverse, middle, center # B. Coeficientes y predicción <br> ## Segundo nivel de interpretación --- ## Interpretación de coeficientes ### Interpretación directa - En el sentido más directo, por una unidad de cambio en la variable independiente, el logit (o log odds) de la variable dependiente cambia en `\(\beta\)` unidades - En el ejemplo, el logit de sobrevivir de las mujeres en relación a los hombres es de 2.467 -- .center[ ## ¿Qué significa esto? ] - Sustantivamente no nos dice mucho, ya que el logit es una transformación de la escala original. - Por lo tanto, para poder interpretar el sentido del coeficiente se requiere volver a la métrica original mediante una transformación inversa. --- ## Interpretación de coeficientes ### Interpretación en términos de chances (Odds Ratio) - Ya que el logit es el log de los OR, para transformalo a OR se debe exponenciar: ```r exp(2.467) ``` ``` ## [1] 11.78703 ``` ### Las chances (odds) de sobrevivir siendo mujer son **11.78** veces más que las de un hombre. --- ## Odds y Logits - Recordemos que el logit se basa en una transformación matemática de una proporción de probabilidades o **odds** (chances): probabilidad de que algo ocurra dividido por la probabilidad de que no ocurra `$$Odds=\frac{p}{1-p}$$` -- Ej. Titanic: - 427 sobrevivientes (41%), 619 muertos (59%) - `\(Odds_{sobrevivir}=427/619=0.41/0.59=0.69\)` **Es decir, las chances de sobrevivir son de 0.69** - Odds de 1 significan chances iguales, menores a 1 son negativas y mayores a 1 son positivas - Propiedad simétrica: un `\(Odd=4\)` es una asociación positiva proporcional a la asociación negativa `\(Odd=1/4=0.25\)` --- ## Odds y Logits En regresión no nos basta con los odds de una variable, sino los que reflejen asociación entre variables. Para esto se utilizan los **Odds-Ratio (OR)** -- **¿Tienen las mujeres más chances de sobrevivir que los hombres?** -- <!-- html table generated in R 3.6.0 by xtable 1.8-4 package --> <!-- Mon Jun 3 00:06:43 2019 --> <table border=1> <tr> <th> </th> <th> Hombre </th> <th> Mujer </th> </tr> <tr> <td align="right"> No sobrevive </td> <td align="right"> 0.795 </td> <td align="right"> 0.247 </td> </tr> <tr> <td align="right"> Sobrevive </td> <td align="right"> 0.205 </td> <td align="right"> 0.753 </td> </tr> </table> -- `$$OR=\frac{p_{m}/(1-p_{m})}{p_{h}/(1-p_{h})}=\frac{0.753/(1-0.753)}{0.205/(1-0.205)}=\frac{3.032}{0.257}=11.78$$` -- ### Las chances de sobrevivir de las mujeres son **11.78** veces más que las de los hombres. --- ## Transformación a Odds `$$Odds_X=e^{\beta_0 + \beta_jX_j}$$` <br> -- - Predicción para **mujeres**= -1.354 + (2.467 * Sexo=1) = 1.113 - Predicción para **hombres**= -1.354 + (2.467 * Sexo=0) = -1.354 -- <br> `$$Odds_{mujer}=e^{1.113}=3.032$$` `$$Odds_{hombre}=e^{-1.354}=0.257$$` -- ### Por lo tanto, la transformación del logit predicho mediante exponenciación permite obtener los Odds. --- ## Transformación a probabilidades predichas `$$p_{mujeres}=\frac{e^{1.113}}{1+e^{1.113}}=\frac{3.04}{4.04}=0.752$$` `$$p_{hombres}=\frac{e^{-1.354}}{1+e^{-1.354}}=\frac{0.258}{1.258}=0.205$$` -- <br> <br> <!-- html table generated in R 3.6.0 by xtable 1.8-4 package --> <!-- Mon Jun 3 00:06:43 2019 --> <table border=1> <tr> <th> </th> <th> Hombre </th> <th> Mujer </th> </tr> <tr> <td align="right"> No sobrevive </td> <td align="right"> 0.795 </td> <td align="right"> 0.247 </td> </tr> <tr> <td align="right"> Sobrevive </td> <td align="right"> 0.205 </td> <td align="right"> 0.753 </td> </tr> </table> --- # Resumen: ¿Qué ganamos con la regresión logística? ### A partir de la estimación logística, con los coeficientes logit podemos: ### 1. Obtener los Odds-Ratio= `\(e^{\beta}\)` ### 2. Obtener los Odds = `\(e^{\beta_0+\beta_X}\)` ### 3. Obtener las probabilidades = `\(\frac{e^{\beta_0+\beta_X}}{1+e^{\beta_0+\beta_X}}\)` --- # Resumen: ¿Qué ganamos con la regresión logística? ### - predicción en el rango de probabilidades (0,1) (que no se logra con regresión OLS) ### - mejor ajuste mediante forma funcional curva (sigmoide) ### - posibilidad de control estadístico en logística múltiple --- class: roja, middle, center # 3. Ajuste --- ## Ajuste: ¿Qué tan bueno es nuestro modelo? - El ajuste de los modelos logísticos se evalúa en general en términos comparativos con otros modelos con más/menos predictores - Estas medidas de comparación se basan en la log verosimilitud (log-likelihood) del modelo, que es una magnitud que se obtiene dado el procedimiento de estimación en regresión logística. - Entre las medidas de ajuste usualmente se consideran: - Devianza (deviance) - Test de razón de verosimilitud (likelihood ratio test) - R2s - Criterio de información de Akaike --- ## Devianza - Devianza =-2*log likelihood: Se utiliza como una medida de los residuos generados por el modelo, comparando con el modelo nulo (sin predictores). En general si disminuye, el modelo es mejor ```r modelo_titanic$null.deviance # devianza modelo sin predictores ``` ``` ## [1] 1414.62 ``` ```r modelo_titanic$deviance # devianza modelo con predictores ``` ``` ## [1] 1102.008 ``` --- ## Test de razón de verosimilitud Compara las verosimilitudes del modelo con otro con menos predictores ```r null_titanic=glm(survived~1, data=tt, family=binomial) anova(modelo_titanic, null_titanic, test ="Chisq") ``` ``` ## Analysis of Deviance Table ## ## Model 1: survived ~ sex ## Model 2: survived ~ 1 ## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 1044 1102.0 ## 2 1045 1414.6 -1 -312.61 < 2.2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` La diferencia entre los modelos es estadísticamente significativa con una probabilidad `\(p<0.01\)`. Por lo tanto el modelo con predictores (sexo) ofrece un mejor ajuste a los datos que un modelo sin predictores. --- # McFadden (pseudo) R2 Se define como: `\(1−[LL(LM)/LL(L0)]\)`, donde - LL es el log likelihood del modelo - LM es el modelo posterior (con predictores) - L0 es el modelo nulo -- ```r logLik(modelo_titanic); logLik(null_titanic) ``` ``` ## 'log Lik.' -551.0042 (df=2) ``` ``` ## 'log Lik.' -707.3102 (df=1) ``` ```r 1-(-551/-707) ``` ``` ## [1] 0.2206506 ``` -- También se puede obtener con la función `PseudoR2` de la librería `DescTools`, junto a otras versiones de pseudo R2s, como "Nagelkerke", "CoxSnell" y "Effron". --- ## Akaike (AIC) AIC - Akaike information criteria, evalua la calidad del modelo a través de la comparación con otros modelos penalizando por la inclusión de predictores (análogo al R2 ajustado): `$$AIC=-2(log-likelihood)+2K$$` Donde K= número de parámetros del modelo (regresores + intercepto) ```r logLik(modelo_titanic) ``` ``` ## 'log Lik.' -551.0042 (df=2) ``` ```r 2*551 ``` ``` ## [1] 1102 ``` `$$AIC=-2(-551)+2(2)=1102+4=1106$$` En sí mismo no es interpretable, solo como criterio comparativo: menor AIC es mejor fit. --- class: roja, right # RESUMEN ### Limitaciones de regresión tradicional (OLS) para variables dependientes dicotómicas ### Dos niveles de interpretación de regresión logística: asociaciones y coeficientes ### Ajuste: medidas comparativas basadas en la log-verosimilitud de los modelos --- class: bottom, left .right[] <br> <br> <br> <br> <br> <br> <br> # Estadística multivariada, 1 sem. 2019 ## Juan Carlos Castillo & Alejandro Plaza ## **Sesión 10**: Regresión Logística 2